二叉树期权定价模型是一种用于对期权进行定价的数值方法。它将未来价格的可能变化简化为一系列向上或向下的二叉树分支，从而逐步推算出期权在到期日的价值，并最终回溯计算出期权的当前价值。与更复杂的模型如Black-Scholes模型相比，二叉树模型更易于理解和实现，特别适合处理那些Black-Scholes模型难以处理的复杂情况，例如包含提前执行条款的美国式期权、期权标的资产的波动率随时间变化的情况，以及分红等因素的影响。虽然它在精确性上可能不如Black-Scholes模型，但其直观性和灵活性使得它成为金融建模中一种有价值的工具。将详细探讨二叉树期货期权定价模型的原理、应用以及优缺点。

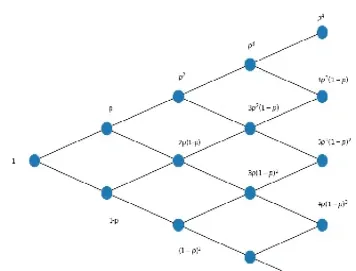
二叉树模型的基本原理

二叉树模型的核心思想是将期权的到期时间划分成若干个小的、相等的时间段。在每个时间段内，标的资产的价格只有两种可能：上涨到一个新的价格或下跌到一个新的价格。这两种可能的概率分别用p和1-p表示。 通过不断重复这个过程，最终可以构建出一棵完整的二叉树，树的节点代表不同时间点上的可能价格，树的叶子节点代表期权到期日的各种可能价格。 每个节点的价值取决于它后续时间段的节点价值及其对应的概率。我们可以通过从到期日反向回溯计算，最终得到期权在初始时间的价值。 具体地，假设在时间段t，标的资产的价格为S_t，向上移动的价格为S_tu，向下移动的价格为S_td，其中u>1, 0u和C_d。在t时间点的期权价值C_t可以用如下公式计算：

C_t = e^-rΔt[p C_u + (1-p)C_d]

其中，r是无风险利率，Δt是每个时间段的长度，e^-rΔt是贴现因子，用于将未来价值折算回现值。 概率p通常根据风险中性概率来计算，其公式为：

p = (e^rΔt - d) / (u - d)

这个公式保证了在风险中性环境下，期权的预期价值等于其现值。

参数的选择与模型的精度

二叉树模型的精度取决于时间段的划分数量和向上/向下移动因子的选择。时间段划分越多，模型的精度越高，但计算量也越大。向上和向下移动因子u和d通常与标的资产的波动率σ和时间段长度Δt有关。常见的选取方法是：

u = e^σ√Δt

d = e^-σ√Δt

这只是一个近似公式，实际应用中，可以选择其他的公式来更好地匹配标的资产的波动率特性。 选择合适的参数对于得到准确的期权价格至关重要。过粗糙的划分会导致明显的误差，而过精细的划分则会增加计算负担，得不偿失。需要根据实际情况权衡精度和计算效率。

处理美国式期权

二叉树模型的一个显著优势是它能够轻松地处理美国式期权。美国式期权可以在到期日之前任何时间执行。在二叉树模型中，我们可以在每个节点上比较期权的内在价值和继续持有期权的价值，选择较大的一个作为该节点的期权价值。这意味着在回溯计算的过程中，我们需要在每个节点上进行一次提前执行与继续持有之间的比较。这种方法使得二叉树模型能够比Black-Scholes模型更准确地对美国式期权进行定价。

二叉树模型的局限性

尽管二叉树模型具有诸多优点，它也有一些局限性。它是一个离散模型，对连续变化的标的资产价格仅进行近似。它对波动率的处理相对简单，尤其是在波动率随时间变化的情况下，精度会受到影响。 当时间段划分非常多时，计算量会变得很大。 对于路径依赖型期权，二叉树模型的应用会变得非常复杂。

与Black-Scholes模型的比较

Black-Scholes模型是一个闭式解模型，它提供了一个精确的欧式期权定价公式。它对标的资产价格的波动率和无风险利率作出了严格的假设，这些假设在实际情况中可能难以满足。 相比之下，二叉树模型是一个数值解模型，它更灵活，可以处理更复杂的场景，例如波动率的随机变化、分红、提前执行等。虽然二叉树模型的精度不如Black-Scholes模型，但在处理这些复杂情况时，它提供了另一种有价值的选择。

应用案例与未来发展

二叉树模型广泛应用于金融衍生品定价，尤其是在处理美国式期权和波动率变化等复杂情况下。它也应用于其他领域，例如实物期权的评估。 未来，二叉树模型的发展方向可能集中在提高模型的效率和精度上。 例如，通过改进参数选择方法，或者结合机器学习技术来优化模型的性能。 将二叉树模型与其他模型结合，例如蒙特卡洛模拟，也可能成为未来研究的重要方向，以期获得更精准和高效的金融衍生品定价方案。